Recursion

Another key idea from functional programming

You learned about it briefly in AP CSA.

Structure of recursion

Base case & recursive case

Base case

The smallest version(s) of problem.

Can be answered directly.

Recursive case

Can only be answered by breaking it down into one or more smaller problems that are then solved by calling the same method.

Technically it doesn’t have to directly call the same method, as long as we end up coming back to the same method.

Make a project in your codespace

./start-project recursion java

Create a file Functions.java.

Factorial

Write a recursive method to compute n!

What is the base case?

What is the recursive case?

Fibonacci

Write the obvious recursive method to compute the nth Fibonacci number.

The Fibonacci sequence is 0, 1, 1, 2, 3, 5, 8, …

I.e. after 0 and 1 each element is the sum of the previous two elements.

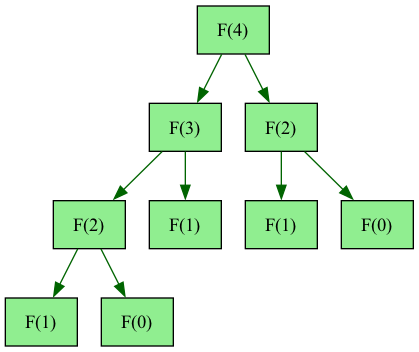
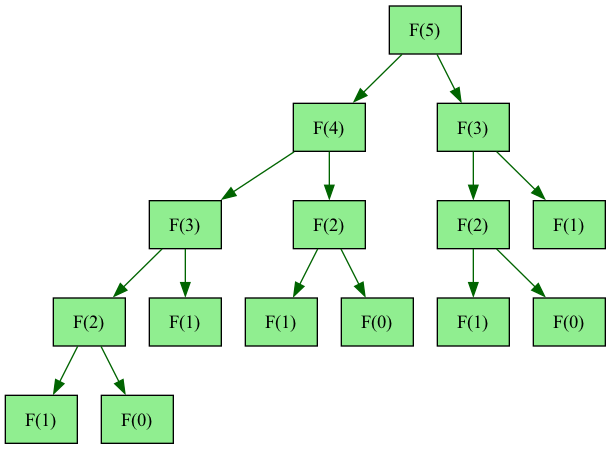
Combinatorial explosion

Sometimes a natural recursive solution does way too much work.

Factorial(4)

This is fine. Each recursive call makes one more recursive call so the growth is just linear.

Actually, that’s maybe not 100% fine. But for now it’s fine.

Fibonacci(4)

Fibonacci(5)

Iterative Fibonacci

Can you write a non-recursive fibonacci method that uses a loop to compute the nth Fibonacci number?

Iterative recursive

Can you write a recursive function (maybe that takes some extra arguments) that follows basically the same sequence of computations as the loop version but using recursion instead of a loop?

Tail recursion

Recursion is, strictly speaking, a superset of iteration. That is, all loops can be turned into recursion.

Turning a recursion into a loop is also possible but may require keeping track of some extra data that would otherwise have been kept track of on the call stack.

Non tail-recursive factorial

private static int factorial(int n) {
  return n * factorial(n - 1);
}

Note that each call is waiting for the result of the recursive call but then has to do some futher computation with the answer it gets back before it can return.

Tail-recursive factorial

private static int factorial(int n) { helper(n, 1); }

private static int helper(int n, int soFar) {
  if (n == 0) {
    return soFar;
  } else {
    return helper(n - 1, soFar * n);
  }
}

In this implementation, the last call (when n == 0) knows the final answer and could return it directly to where factorial is waiting for it.

Change

Write a method that takes two arguments, an amount of money and a list of coin denominations (e.g. 1, 5, 10, 25, 50) and returns the number of ways you can make that amount of money with some combination of the given kinds of coins.

To start with, don’t worry about combinatorial explosion. Just get the basic recursion working.

Change hints

This method might be handy:

public static <T> List<T> dropFirst(List<T> list) {
  return list.subList(1, list.size());
}

Quick check if your method is working:

change(100, List.of(1, 5, 10, 25, 50)) => 292

Iterative change

Try running your recursive method on larger amounts and see how the runtime grows.

Can you use a technique similar to the one you used to write an iterative fibonacci method to write an iterative change method?